Lab 9 – Million Monkeys with Typewriters

Lab 9 – Million Monkeys with Typewriters

• Lab 9 Home
• Part 1
• Part 2
• Part 3
• Submission

Part 2 – Text Generation

Markov Models

You will be using a Markov model for the somewhat silly purpose of generating stylized pseudo-random text; however, Markov models have plenty of “real” applications in speech recognition, handwriting recognition, information retrieval, and data compression.

Our Markov model is going to generate one character of our output at a time. In order to determine what this next character is, we will need to look at the sample text to determine what character is most likely to occur at this point in the text. In order to determine what character is most likely to occur, we look at the last few characters we generated, and try to find those character in our sample text. Hopefully we’ll find it a bunch of times, and from these occurrences we try to figure out what character should occur next.

For example, suppose we have already generated the text I do not like them, and we want to determine the next character. Then, we may look in the sample text for all occurrences of the substring ke them, , and we may find that the substring occurs 10 times: 7 times it is followed by Sam-I-am, 2 times it is followed by on a boat, and once it is followed by on a house. Then, with 7/10 probability, the next character is an S, and with 3/10 probability it is an o.

Now if you think about it, the further back we look in the text, the more our generated text will resemble the original. However, looking farther back requires a lot more work and space, and produces less interesting text. So there are trade-offs to consider. The Markov model formalizes this notion as follows.

An order 0 Markov model looks in the sample text for the previous 0 characters of our generated text. That is, given an input text, you compute the Markov model of order 0 by counting up the number of occurrences of each letter in the input and use these as the frequencies. For example, if the input text is agggcagcgggcg, then the order 0 Markov model predicts that each character is a with probability 2/13, c with probability 3/13, and g with probability 8/13. This has the effect of predicting that each character in the alphabet occurs with fixed probability, independent of previous characters.

Characters in English text are not independent, however. An order k Markov model looks back at the previous k characters in the generated text, and bases its prediction on that substring of length k. That is, given an input text, you compute a Markov model of order k by counting up the number of occurrences of each letter that follows each sequence of k letters. For example, if the text has 100 occurrences of th, with 50 occurrences of the, 25 occurrences of thi, 20 occurrences of tha, and 5 occurrences of tho, the order 2 Markov model predicts that the next character following th is e with probability 1/2, i with probability 1/4, a with probability 1/5, and o with probability 1/20.

Representation of a Markov model

Mathematically, an order k Markov model is a set of states and transitions between states. Each state represents the most recent k characters that have been generated. Each transition is associated with a character to generate and the probability of generating that character.

Let’s look at an example. If k is 2 and the input string is agggcagcgggcg, then the Markov model will be constructed by looking at each substring of length 2 and looking at the letter that follows it.

ag ↦ g
gg ↦ g
gg ↦ c
gc ↦ a
ca ↦ g
ag ↦ c
gc ↦ g
cg ↦ g
gg ↦ c
gc ↦ g

This is the basis for our transitions. Notice that since the final two characters in the input string aren’t followed by a character, they’re not included in the list. If you look carefully at the list, you’ll notice that there are only five distinct 2-letter substrings, ag, gg, gc, ca, and cg. These are our states.

We can summarize our list by counting how many times each k-letter substring is followed by a given character.

ag ↦ 1 c, 1 g
ca ↦ 1 g
cg ↦ 1 g
gc ↦ 1 a, 2 g
gg ↦ 2 c, 2 g

That is, ag is followed by c one time and by g one time; gc is followed by a one time and by g two times in our input string.

We can turn these counts into probabilities. ag is followed by c 50% of the time and by g 50% of the time. gc is followed by a 33% of the time and by g 67% of the time. These are our transitions. They’re called transitions because using them, we can transition from one state to another. For example, if we start with the text ag, then we say that our model is in state ag. We’ll generate a c with 50% probability which will bring the model to state gc (because our output string is now agc and gc are the last k = 2 characters). We can represent the Markov model graphically like this.

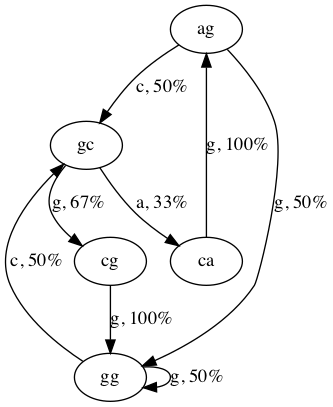
The ovals are the states (which are the final k characters in our generated string) and the arrows are the transitions which are labeled with the character to generate in a given state along with its probability.

We started in state ag and generated a c which took us to state gc. Now, with 67% probability, we’ll generate a g bringing our output string to agcg and taking us to state cg. This process continues until we’ve generated as much output as we desire.

Implementing a Markov model

To represent an order k Markov model in code, we are going to keep a hash map from length-_k_ strings to State objects. Each State object will maintain a hash map from characters to integers to represent the transitions. Continuing our example, the State for gc will have a map:

a ↦ 1
g ↦ 2

For efficiency, each State maintains a count that is the sum of all of the values in its transitions map. E.g., for gc, count is 3. This implicitly encodes the probability of generating each character. To compute the probability of generating a g in a given State, we’d look up g in the transitions map and divide the value by the count. For the State gc, that gives 2/3. (We’ll see a simple way to select one of the characters to generate below that uses the counts rather than the frequency.)

To build the model, we need to train it on an input string. MarkovModel has a method train(input) that you will implement. The train(input) method will look at each length-(k + 1) substring of its input and call the add(prefix, suffix) where prefix is the first k characters of the substring and suffix is the final character. The add() method will use the prefix to look up (or create) the corresponding State in its states map and then call state.add(suffix). The State’s add(suffix) method will lookup the suffix in its transitions map and increment the count.

Start by implementing the MarkovModel’s train() and add() methods as well as the State’s add() method. Ignore generate() and randomSuffix() for now; we’ll return to them when we get to generating text shortly.

public void train(String input)

Iterate over the input string starting with index this.order and use input.charAt(index) to get the suffix and input.substring(index - this.order, index) to get the prefix. Call add(prefix, suffix).

public void add(String prefix, char suffix)

Look up or create a State corresponding to prefix in this.states. Call add(suffix) on it.

void add(char suffix)

This is in the State class. This method should increment the integer in the transitions map corresponding to suffix. Don’t forget to increment the State’s count variable as well.

Once you’ve done this, you should be able to run MarkovModel. It requires two command line parameters. The first parameter is the order of the model. The second parameter is the path to a file to use to train. Try it with command line arguments: 2 samples/example.txt

Generator

Now that we can build a Markov model, it’s time to use it to generate some text! You’ll need to implement MarkovModel’s generate() method and State’s randomSuffix() method as well as create a new class which will build a model and then generate some text.

To generate text, we need a pseudorandom number generator. Fortunately, Java provides one for us called SecureRandom. (There are others; they should never be used.) Both of the methods take a parameter rand of type Random which is a super class of SecureRandom.

public String generate(String prefix, int length, Random rand)

This method generates a string of length length that starts with prefix. The prefix must be a string whose length is the same as the order of the model.

Start by getting the initial state by looking prefix up in the states map. If the initial state is null, throw an IllegalArgumentException.

Create a StringBuilder that’s initialized to the prefix:

StringBuilder sb = new StringBuilder(prefix);

In a loop, use the StringBuilder’s substring() method to get a string of length k where k is the order of the model from the end of the StringBuilder. Look up the State corresponding to the substring. If it’s not in the map, then using the initial State instead. Call state.randomSuffix(rand) which returns a character. Append it to the string builder.

Once the string is long enough, use sb.toString() to construct a string and return it.

char randomSuffix(Random rand)

This method should iterate over the entries in this.transitions.entryList() and return one of the characters at random. The tricky part is that each character should be returned with the appropriate probability.

Fortunately, there’s a simple method we can use to do this. Imagine the state has the following mapping

' ' ↦ 9
'a' ↦ 3
'e' ↦ 1
'r' ↦ 7

That is, during training, the space was the next character 9 times, a was the next character 3 times, e was the next character 1 time, and r was the next character 7 times. Since the sum of those (the state’s count variable) is 20, we can generate a random integer x in the range [0, 20). Now, we can check in order:

• if x < 9, then return a space
• if x < 12, then return a
• if x < 13, then return e
• if x < 20, then return r

Since x is definitely less than 20, it will return one of those. We can easily turn this into a loop by noticing that after each check, we can decrement x by the value we were comparing against. This gives the algorithm.

• if x < 9, then return a space, otherwise set x to x - 9
• if x < 3, then return a, otherwise set x to x - 3
• if x < 1, then return e, otherwise set x to x - 1
• if x < 7, then return r, otherwise set x to x - 7

To generate x, use

int x = rand.nextInt(this.count);

There should only be a single call to rand.nextInt() per call to randomSuffix().

Finally, create a class TextGenerator that takes as command line parameters an integer order, an integer length, and a filename file, and prints out length characters according to the Markov model of the given order trained on the contents of file.

Testing

You should test out your text generation with very simple inputs first, such as with a file containing flippyfloppies and small order and length.

Once you get that working, you should try it on some of the files provided in samples. You will find that the generated text starts to sound more and more like the original text as you increase the order of the model, as illustrated in the examples in the next part. As you can see, there are limitless opportunities for amusement here. Try your model on some of your own text, or find something interesting on the Internet.

« Previous Next »